
520R-MX PCIe Card with Intel Stratix 10 MX FPGA
PCIe FPGA Card 520R-MX Stratix 10 FPGA Board with HBM2 and 480Gbps Optical Input Optimized for sensor processing applications with massive real-time data ingest requirements
Convolutional Neural Networks (CNNs) have been shown to be extremely effective at complex image recognition problems. This white paper discusses how these networks can be accelerated using FPGA accelerator products from BittWare, programmed using the Intel OpenCL Software Development Kit. This paper then describes how image categorization performance can be significantly improved by reducing computation precision. Each reduction in precision allows the FPGA accelerator to process increasingly more images per second.
Caffe is a deep learning framework made with expression, speed, and modularity in mind. It is developed by the Berkeley Vision and Learning Center and by community contributors.
The Caffe framework uses an XML interface to describe the different processing layers required for a particular CNN. By implementing different combinations of layers a user is able to quickly create a new network topology for their given requirements.
The most commonly used of these layers are:
By porting these 4 layers to the FPGA, the vast majority of forward processing networks can be implemented on the FPGA using the Caffe framework.
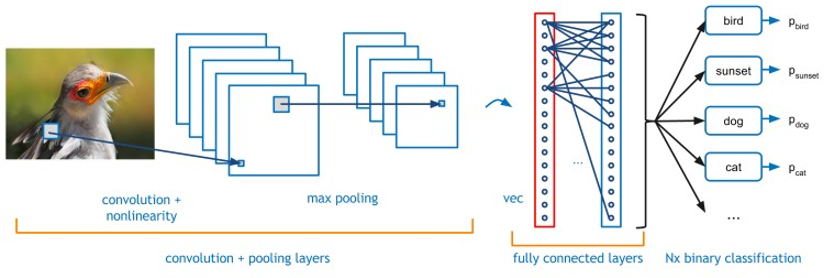
Figure 1 : Example illustration of a typical CNN – Convolutional Neural Network
AlexNet is a well known and well used network, with freely available trained datasets and benchmarks. This paper discusses an FPGA implementation targeted at the AlexNet CNN, however the approach used here would apply equally well to other networks.
Figure 2 illustrates the different network layers required by the AlexNet CNN. There are 5 convolution and 3 fully connected layers. These layers occupy > 99% of the processing time for this network. There are 3 different filter sizes for the different convolution layers, 11×11, 5×5 and 3×3. To create different layers optimized for the different convolution layers would be inefficient. This is because the computational time of each layer differs depending upon the number of filters applied and the size of the input images. due to the number of input and output features processed. However, each convolution requires a different number of layers and a different number of pixels to process. By increasing the resource applied to more compute intensive layers, each layer can be balanced to complete in the same amount of time. Hence, it is therefore possible to create a pipelined process that can have several images in flight at any one time maximizing the efficiency of the logic used. I.e. most processing elements are busy most of the time.
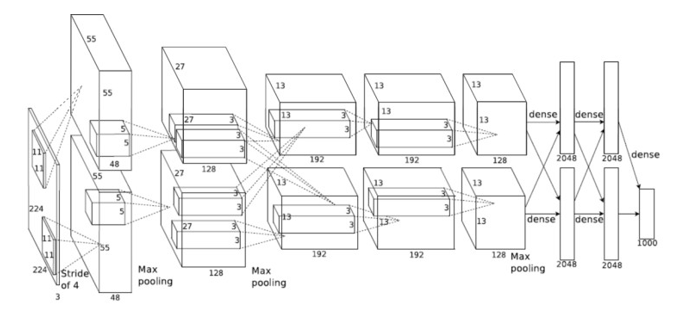
Figure 2 : AlexNet CNN – Convolutional Neural Network
Table 1 shows the computation required for each layer of the Imagenet network. From this table it can be seen that the 5×5 convolution layer requires more compute than the other layers. Therefore, more processing logic for the FPGA will be required for this layer to be balanced with the other layers.
FPGA devices have two processing regions, DSP and ALU logic. The DSP logic is dedicated logic for multiply or multiply add operators. This is because using ALU logic for floating point large (18×18 bits) multiplications is costly. Given the commonality of multiplications in DSP operations FPGA vendors provided dedicated logic for this purpose. Intel have gone a step further and allow the DSP logic to be reconfigured to perform floating pointer operations. To increase the performance for CNN processing it is necessary to increase the number of multiplications that be implemented in the FPGA. One approach is to decrease the bit accuracy.
| ImageNet Layer | Multiply Adds (M) |
| Convolution (11×11) | 130 |
| Convolution (5×5) | 322 |
| Convolution (3×3) 1 | 149 |
| Convolution (3×3) 2 | 112 |
| Convolution (3×3) 3 | 75 |
| Inner Product 0 | 37 |
| Inner Product 1 | 17 |
| Inner Product 2 | 4 |
Table 1 : ImageNet layer computation requirements
Most CNN implementations use floating point precision for the different layer calculations. For a CPU or GPGPU implementation this is not an issue as the floating point IP is a fixed part of the chip architecture. For FPGAs the logic elements are not fixed. The Arria 10 and Stratix 10 devices from Intel have embedded floating DSP blocks that can also be used as fixed point multiplications. Each DSP component can in fact be used as two separated 18×19 bit multiplications. By performing convolution using 18 bit fixed logic the number of available operators doubles compared to single precision floating point.
Layer(s) | Size | Filter Size | No Filters |
CONV x2 | 416×416 | 3×3 & 1×1 | 32,64 |
CONV x3 | 208×208 | 3×3 & 1×1 | 64,128 |
CONV x5 | 104×104 | 3×3 & 1×1 | 64,128 |
CONV x17 | 52×52 | 3×3 & 1×1 | 128,256 |
CONV x17 | 26×26 | 3×3 & 1×1 | 256,512 |
CONV x15 | 13×13 | 3×3 & 1×1 | 512×1024 |
Up-sample & route | 26×26 | 3×3 & 1×1 | 256 |
CONV x7 | 26×26 | 3×3 & 1×1 | 256,512 |
Up-sample & route | 52×52 | 3×3 & 1×1 | 128 |
CONV x7 | 52×52 | 3×3 & 1×1 | 128,256 |
Figure 3 : Arria 10 floating point DSP configuration
If a reduced precision floating point processing is required it is possible to use half precision. This requires additional logic from the FPGA fabric, but doubles the number of floating point calculations possible, assuming the lower bit precision is still adequate.
One of the key advantages of the pipeline approach described in this white paper is ability to vary accuracy at different stages of the pipeline. Therefore, resources are only used where necessary, increasing the efficiency of the design.
Depending upon the CNNs application tolerance, the bit precision can be reduced further still. If the bit width of the multiplications can be reduced to 10 bits or less, (20 bit output) the multiplication can then be performed efficiently using just the FPGA ALU logic. This doubles the number of multiplications possible compared to just using the FPGA DSP logic. Some networks maybe tolerant to even lower bit precision. The FPGA can handle all precisions down to a single bit if necessary.
For the CNN layers used by AlexNet it was ascertained that 10 bit coefficient data was the minimum reduction that could be obtained for a simple fixed point implementation, whilst maintaining less than a 1% error versus a single precision floating point operation.
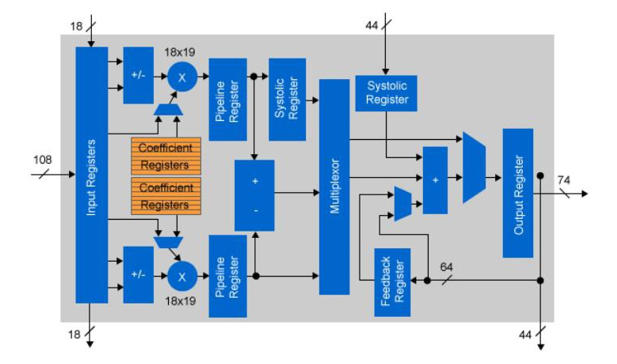
Figure 4 : Arria 10 fixed point DSP configuration
Using a sliding window technique, it is possible to create convolution kernels that are extremely light on memory bandwidth.
Figure 5 illustrates how data is cached in FPGA memory allowing each pixel to be reused multiple times. The amount of data reuse is proportional to the size of the convolution kernel.
As each input layer influences all output layers in a CNN convolution layer it is possible to process multiple input layers simultaneously. This would increase the external memory bandwidth required for loading layers. To mitigate the increase all data, except for coefficients, is stored in local M20K memory on the FPGA device. The amount on chip memory on the device limits the number of CNN layers that can be implemented.
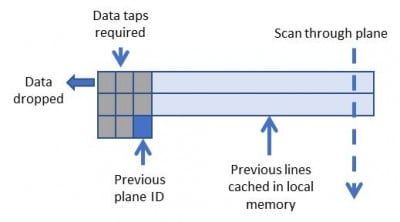
Figure 5 : Sliding window for 3×3 convolution
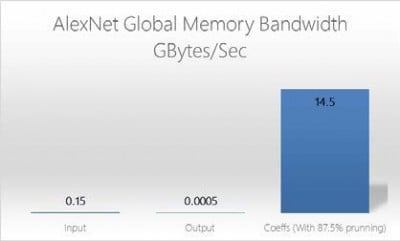
Figure 6 : OpenCL Global Memory Bandwidth (AlexNet)
Depending upon the amount of M20K resource available it is not always possible to fit a complete network on a single FPGA. In this situation, multiple FPGA’s can be connected in series using high speed serial interconnects. This allows the network pipeline to be extended until sufficient resource is available. A key advantage to this approach is it does not rely on batching to maximize performance, therefore the latency is very low, important for latency critical applications.
Balancing the time taken between layers to be the same requires adjusting the number of parallel input layers implemented and the number of pixels processed in parallel.
Resource | AlexNet 5×5 Convolution Layer (float) | AlexNet 5×5 Convolution Layter (16-bit) |
Register | 346,574 | 129,524 |
DSP Blocks | 1,203 | 603 |
RAM Blocks | 1,047 | 349 |
Figure 9: Resources for 5×5 convolution layer of Alexnet
Most CNN features will fit within a single M20K memory and with thousands of M20Ks embedded in the FPGA fabric, the total memory bandwidth available for convolution features in parallel is in the order of 10’s Terabytes/sec.
Resource | GX1150 | GX2800 |
Logic Elements (K) | 1,150 | 2,753 |
ALM | 427,200 | 933,120 |
Register | 1,708,800 | 3,732,480 |
Variable Precision DSP Block | 181,5 | 5,760 |
18×19 Multiplier | 3,036 | 11,520 |
Figure 7 : Arria 10 GX1150 / Stratix 10 GX2800 resources
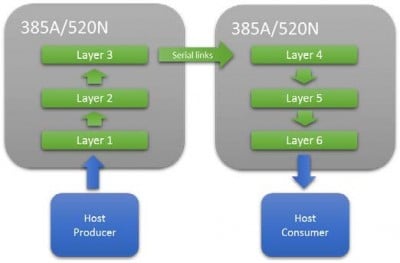
Figure 8 : Extending a CNN Network Over Multiple FPGAs
Figure 9 lists the resources required for the 5×5 convolution layer of Alexnet with 48 parallel kernels, for both a single precision and 16 bit fixed point version on an Intel Arria10 FPGA. The numbers include the OpenCL board logic, but illustrate the benefits of lower precision has on resource.
Processing of a fully connected layer requires a unique coefficient for each element and therefore quickly becomes memory bound with increasing parallelism. The amount of parallelism required to keep pace with convolutional layers would quickly saturate the FPGA’s off chip memory, therefore it is proposed that his stage of the input layers either batched or pruned.
As the number of elements for an inner product layer is small the amount of storage required for batching is small versus the storage required for the convolution layers. Batching layers then allows the same coefficient to be used for each batched layer reducing the external memory bandwidth.
Pruning works by studying the input data and ignoring values below a threshold. As fully connected layers are placed at the later stages of a CNN network, many possible features have already been eliminated. Therefore, pruning can significantly reduce the amount of work required.
The key resource driver of the network is the amount of on chip M20K memories available to store the outputs of each layer. This is constant and independent of the amount of parallelism achieved. Extending the network over multiple FPGA’s increases the total amount of M20K memory available and therefore the depth of the CNN that can be processed.
The unique flexibility of the FPGA fabric allows the logic precision to be adjusted to the minimum that a particular network design requires. By limiting the bit precision of the CNN calculation the number of images that can be processed per second can be significantly increased, improving performance and reducing power.
The non-batching approach of FPGA implementation allows single frame latency for object recognition, ideal for situations where low latency is crucial. E.g. object avoidance.
Using this approach for AlexNet (single precision for layer 1, then using 16 bit fixed for remaining layers), each image can be processed in ~1.2 milliseconds with a single Arria 10 FPGA, or 0.58 milliseconds with two FPGAs in series.

PCIe FPGA Card 520R-MX Stratix 10 FPGA Board with HBM2 and 480Gbps Optical Input Optimized for sensor processing applications with massive real-time data ingest requirements

PCIe Gen4 data mover IP from Atomic Rules. Achieve up to 220 Gb/s using BittWare’s PCIe Gen4 cards, saving your development team when you need more performance than standard DMA. Features: DPDK and AXI standards, work with packets or any other data format, operate at any line rate up to 400 GbE.

Intel® oneAPI™ High-level FPGA Development Menu Evaluating oneAPI Accelerator Cards ASPs More Info Contact/Where to Buy Is oneAPI Right for You? You may already know

REFERENCE DESIGN MAU Accelerator for AI Financial Trading Models Ultra-low Latency, High Throughput Machine Learning Inference Well suited to a range of applications in financial