Article

同態加密加速

FPGA 加速支援這種獨特的解決方案，允許在不解密或共用密鑰的情況下對加密數據進行計算

傳統加密限制

加密數據是醫療文件或財務等敏感資訊的必要條件，其數量呈指數級增長。理想情況下，這些數據將存儲在經濟的公共雲基礎設施中，包括處理功能，例如在資料庫中查找記錄。但是，由於加密，這意味著雲存儲供應商將需要私鑰，並且能夠看到搜索詞和結果。這種共用金鑰和對私人資訊的暴露會帶來重大的安全風險。

使用雲端儲存和計算的傳統加密

在上面的範例中，加密資料庫存儲在公共雲伺服器上。為了檢索數據，例如搜索，雲系統必須擁有解密資料庫的私鑰，而且還要看到搜索詞和結果。雖然這些數據在通過不安全的鏈接傳遞之前是加密的，但風險在於雲供應商擁有私鑰，並且安全性依賴於他們的系統不會受到損害。

由於這些限制，許多類型的高度安全數據（如醫療記錄）無法使用公共雲基礎架構。

同態加密

然而，幾十年前的技術允許處理加密數據，例如文本搜索， 而無需 解密或提供對私鑰的訪問。它還允許對處理請求（例如搜索詞）和結果進行加密。存儲供應商可以毫無風險地存儲和處理敏感的加密數據。

這種技術稱為 同態加密（HE）， 可用於計算需求不斷增加的幾個級別。事實上，在像BittWare的IA-440i 這樣的功能強大的FPGA卡可用之前，同態加密所需的計算嚴重限制了實際用例。

同態加密用例

雖然我們提到了資料庫搜索，但同態加密還有許多其他潛在用途：

多個使用者協作處理加密數據，沒有數據本身暴露的風險，因為它從未以明文形式存儲甚至傳輸。
組織可以在網站之間自由共用敏感數據，而無需共用解密金鑰的風險。
資料庫可以以完全加密的狀態存儲在公共雲上，並且仍然可以被積極使用;雲的破壞只會暴露加密的數據，而無法訪問私鑰。
機器學習圖像或音訊搜索可以由公共推理計算資源執行，搜索本身、結果甚至數據源池都無法從計算/存儲提供程式中辨別出來。

工作原理

同態加密方案通常遵循以下兩種方法之一：

平整高等教育方案

這種方法允許在內部誤差（所有HE方案中存在）變得太大之前執行一定量的處理。如果事先知道所需的處理深度，用戶可以創建具有適當公差的HE方案。這樣做的好處是確保只執行最少的處理量，從而提高輸送量。

全高金計劃

該方案也受到雜訊增加的影響，但使用一種稱為“引導”的技術來消除任何錯誤累積，以免它變得太大。Boostrapping非常慢，儘管最近在加速這一性能瓶頸方面取得了一些進展。

選擇使用HE方案在很大程度上取決於使用者的問題情況。因此，一種解決方案不太可能適合所有人。在HE中處理加密數據也非常慢，需要 顯著加速 才能使用。幸運的是，FPGA非常擅長加密方案所需的計算類型，並且足夠靈活，可以有效地處理任何合適的HE方案。

FPGA 加速同態加密系統

使用支援乙太網的FPGA卡，用戶可以發送加密的資料庫請求。FPGA 上的 HE 邏輯將此請求轉換為儲存在附加持久記憶體中的加密資料庫中的相應查找。在任何時候，駭客都無法提取有用的信息，從而允許資料庫在公共領域內自由提供。由於資料庫採用加密格式，如果非法訪問數據，則無法提取敏感資訊或演算法IP。

使用同態加密的機器學習推理

同態加密不僅限於基於文字的資料庫應用程式。 上述相同的 FPGA 加速系統可以提供加速即計算服務，例如機器學習（ML）推理。例如，在醫療領域，可以將患者 X 射線（作為圖像）發送到基於雲的 ML 模型以檢測異常。但是，與資料庫範例一樣，此類查找需要將個人醫療資訊（X 射線圖像）發送給共用 ML 模型供應商，該提供者必須解密圖像才能執行推理。相反，請看下圖的可能性，其中顯示了FPGA加速的HE和推理系統，該系統為許多使用者提供安全查找：

在這個HE安全的系統中，患者的X射線，訓練的ML模型和結果將在共用提供者的系統中保持加密。與資料庫搜索範例一樣，理想的主機將處理許多使用者和對共用資源的查找。對於保護此類系統的同態加密，佈局與資料庫搜索範例非常相似。

當今的性能限制

請注意，即使通過FPGA進行高性能加速，如今的HE系統也比未加密的同類系統慢幾個數量級。因此，需要做更多的工作來縮小這種性能差距，以便更廣泛地採用。

更深入：同態加密簡史

在實現完全同態加密（FHE）之前，一些眾所周知的加密方案已經表現出一些部分同態能力。加密方案RSA表現出乘法同態，因為兩個加密的密文可以相乘，並在解密時返回等效的明文乘法結果。

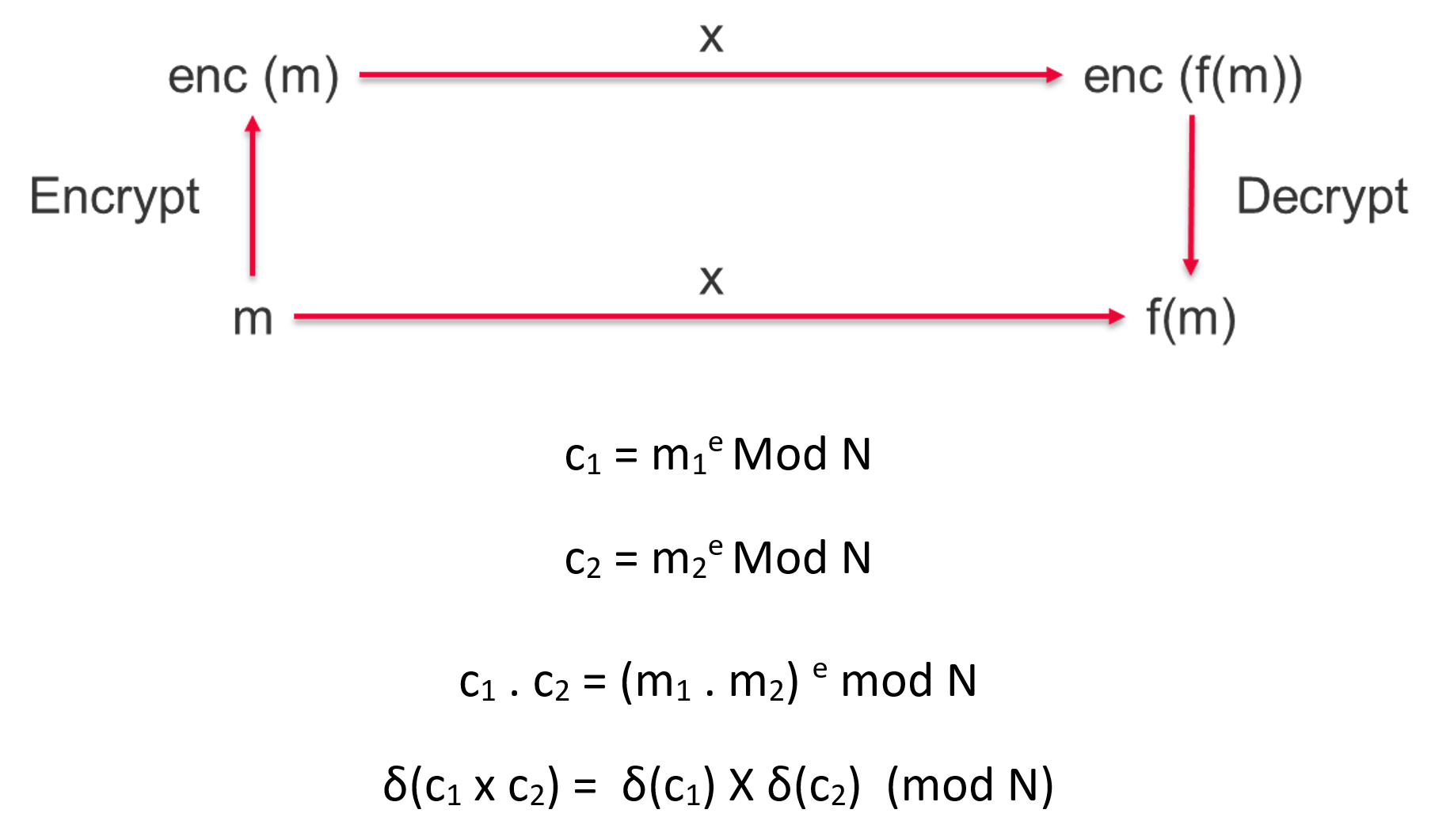
而Paillier密碼系統是附加加密方案的一個例子。這可以寫成如下...

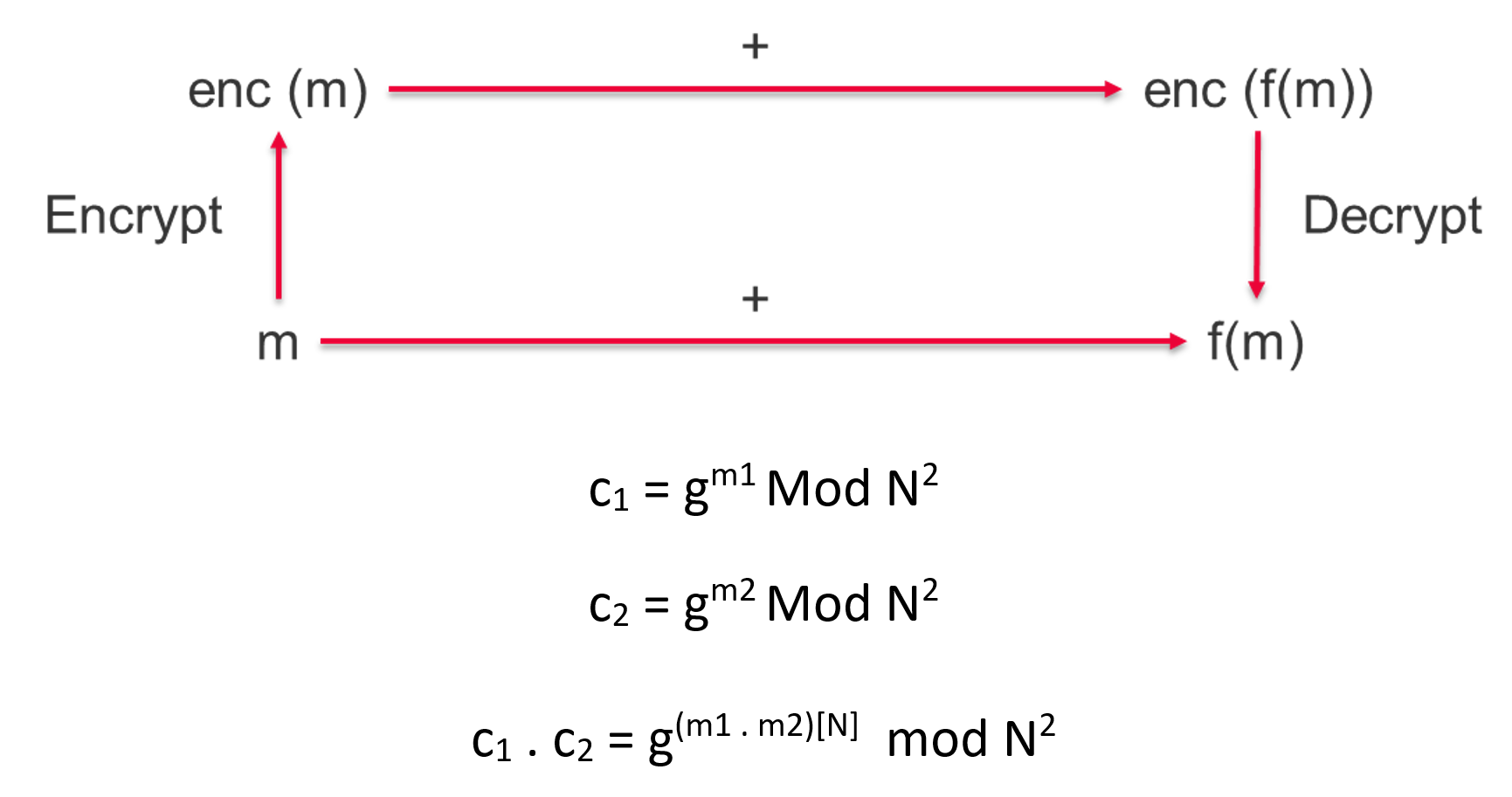
如前所述，完全同態加密（FHE）方案可以執行加法和乘法運算。在這種情況下，允許重複乘法或添加密文，同時仍允許恢復原始明文。

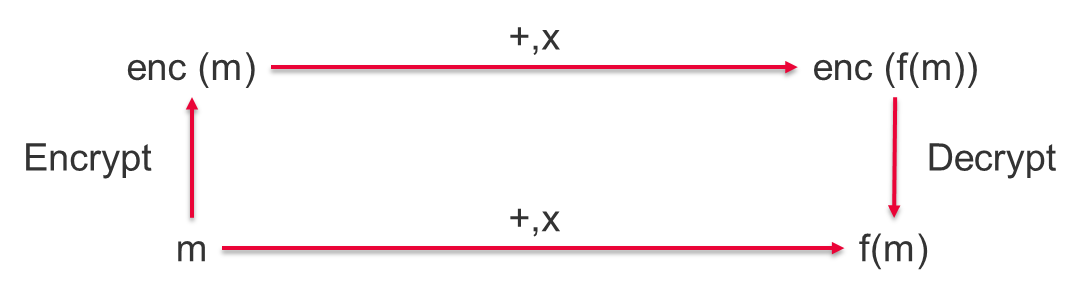
如果HE方案允許乘法和加法，那麼它就能夠執行邏輯NAND門，從而執行任何邏輯電路。

DGHV全同態加密方案

最早的FHE計劃之一是DGHV計劃。這依賴於非常大的密文來確保良好的安全性。加密和解密方案由以下等式表示。

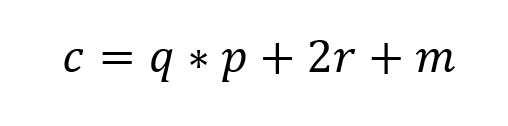
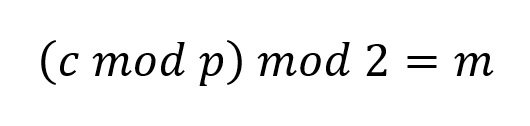
密文必須非常大才能進行良好的加密，10 百萬位，密鑰 p 數千位和較大的雜訊值。為了確保加密方案不容易受到線性代數攻擊，必須考慮引入雜訊（r）。具體如下所述。

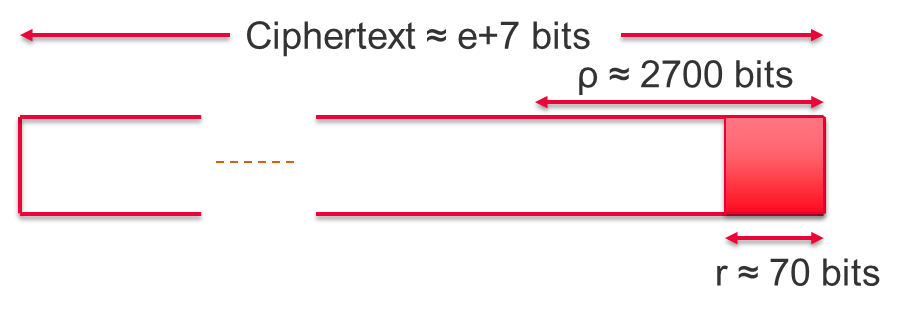
使用如此大的密文顯然存在性能問題，單個明文位擴展到數百萬個密文位，這使得它在實際用例中不切實際。然而，這是最早創建並重新啟動HE學術研究的功能HE方案之一。

DGHV方案的另一個問題是雜訊增長，這是由添加到加密中所需的隨機因數產生的。在這種情況下，密文的添加會使此雜訊增加一個比特，但是每次應用密文時，乘法會使雜訊加倍。

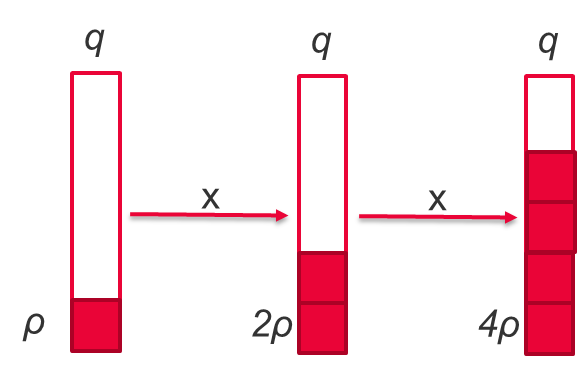
該圖說明瞭相對於金鑰大小 q 的乘法雜訊 ρ 加倍。一旦雜訊超過q，就無法再恢復明文而沒有錯誤。這意味著在流程中斷之前，我們只能處理有限數量的操作。

為了解決此錯誤增長，使用了一種稱為引導的技術。引導可以通過加密邏輯傳遞密文來消除雜訊，使用共用公鑰進行加密。這相當於解密密文（消除噪音）並重新加密，但是由於公鑰不能用於恢復原始明文，因此數據始終保持私有。這個過程在計算上是昂貴的，但可以消除雜訊，允許無限數量的加密計算：完全同態加密（FHE）方案。

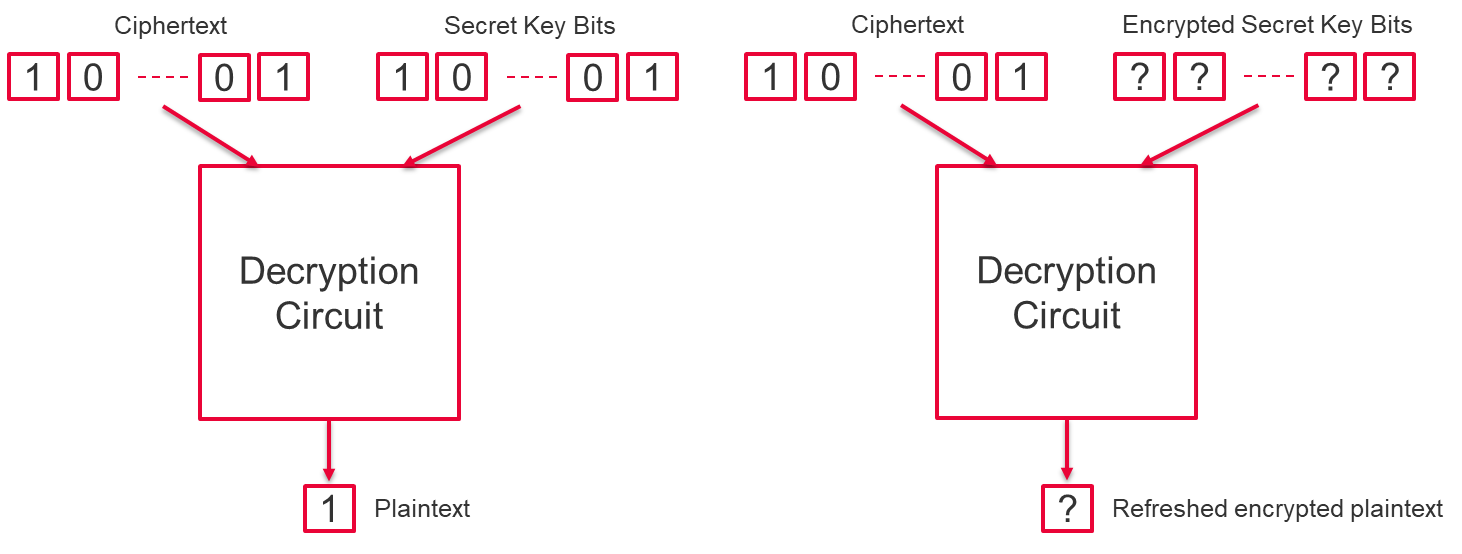
錯誤學習（LWE）

誤差學習（LWE）方案基於多項式計算，其中加密金鑰現在是 N 次多項式的係數。多項式的係數位於具有字大小素數 q 的有限域中。為了增加安全性，必須將雜訊（e）添加到系統中，否則使用線性代數可以輕鬆求解該方案。

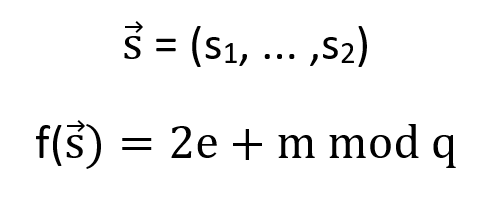
兩個多項式的相加創建相同次數的第三個多項式;然而，兩個多項式的乘法會產生（n+1）² 係數的二次多項式。為了糾正多項式項數的增長，使用了一種稱為重新線性化的技術。多項式的二次項是公開的，然後可以使用二進位分解從結果中減去，再次將展開多項式減少到（n+1）係數。這種乘法的雜訊增長與DGHV相同，但是可以使用稱為模數切換的技術來減少其影響。

可以證明，按新素數縮放係數，使新係數“c”等價，使得c_new = c mod 2，解密結果保持不變。這種關係可用於將雜訊的指數增長轉換為線性增長，從而允許在雜訊增長變得太大之前對密文執行更多操作（見下圖）。

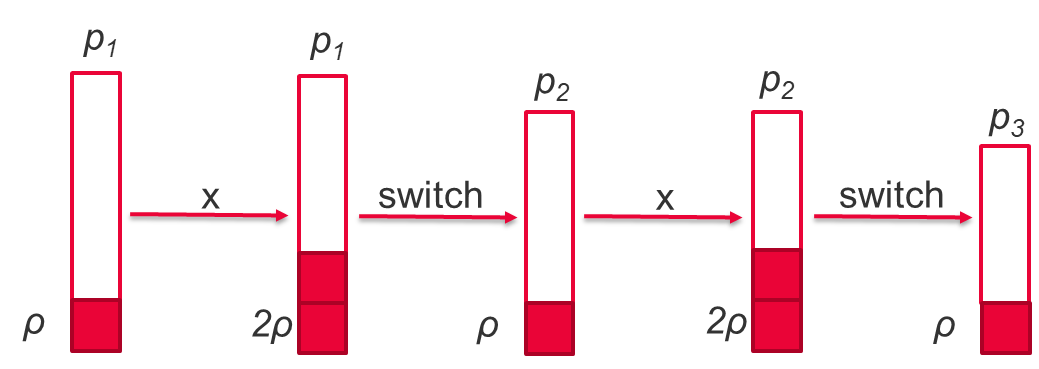
這就是所謂的水準FHE。如果我們知道計算的深度，我們可以選擇初始模量的大小，使其足夠大，以解決給定的問題，從而避免昂貴的自舉階段。

帶錯誤的環學習（RLWE）

LWE 方案的擴展是使用多項式環，其中 N 是 2 的冪。多項式現在存在於環中 .在這種情況下，將兩個多項式相加或相乘，係數仍會減少素模。乘法后，2N 係數通過除以（X 時取餘數來減少^N + 1).

多項式的乘法是此HE實現的主要瓶頸，因為係數的數量通常在N = [2¹⁰， 2¹⁴]範圍內。多項式乘法的優化是負迴圈數論變換（NTT）。這將計算次數從 N N 減少到 Nlog（^N ）。NTT 是有限整數域上的快速傅立葉變換（FFT）。

將兩個多項式 f（x）和 g（x）相乘，然後變成...

InvNTT （FwdNTT（f（x）） * FwdNTT（g（x）））

公共領域介面

公共領域有多個 HE API 可用，主要針對 CPU 進行了優化。以下是一些範例：

隨著性能的提高和更快的技術實現，大多數都處於連續流動狀態。

英特爾 HEXL – FPGA

英特爾還有一個並行的 FPGA 分支到他們的 HEXL 庫。面向 FPGA 的英特爾同態加密加速庫（HEXL-fpga）是一個開源庫，提供 HE 函數的一些 FPGA 實施範例。

目前包含在 FPGA API 中的運算符如下：

二元乘法：兩個多項式的乘法
金鑰開關：切換公共加密金鑰或參數
正向和逆負循環數論變換（NTT）

這些使用戶能夠在FPGA上試驗不同的HE工作流程。BittWare USM（統一共用記憶體）BSP與此庫相容。

結論

同態加密的潛在好處是顯著的;更好地利用公眾共用資源處理高風險數據，例如用於醫療和金融領域的數據。HE正在不斷發展，以解決新技術的性能問題。

FPGA 是幫助實現 HE 採用的理想技術，因為它們具有高度的靈活性和高性能架構。像IA-440i 這樣的BittWare卡非常適合幫助客戶推動同態加密從學術研究到實際部署的轉變。

瞭解有關我們採用 Agilex 技術的 FPGA 加速器卡的更多資訊→

縮寫

HE：同態加密

RSA：里維斯特、沙米爾和阿德曼

FHE：完全同態加密

DGHV： Digi Gentry Halevi Vaikuntanathan

RLWE ：帶錯誤的環學習

Article

同態加密加速

傳統加密限制

使用雲端儲存和計算的傳統加密